Originally Posted by
SeeDRankLou

Dammit, you're right.
The proof of this part of the theorem is actually one of the problems at the end of the section in the book. It's an odd question, so the answer is in the back of the book. The question goes:
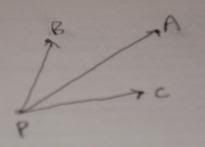
"Suppose that points P, A, B and C all lie on the same plane. Show that vectors a=PA, b=PB and c=PC are coplanar vectors."
And the only thing the back of the book says for this answer is
"a dot (b x c) = 0"
I looked up the book online, and it gives the answer to all questions in the book in more detail than in the back of the book. And still, for this question all it says is
"a dot (b x c) = 0"
Is it really simple enough to just say that because the points all lie on the same plane, then PA dot (PB x PC) = 0, so a, b and c are all on one plane and thus coplanar?




 Reply With Quote
Reply With Quote